Chapter 4 - Worked Solutions

to selected extension questions from the OUP text Senior Physics - Concepts in Context by Walding, Rapkins and Rossiter

t₂ (above the surface) = 2t₁ (on surface)

s₁ = ut₁ + ½ g₁t₁²

s₁ = ut₂ + ½ g₂t₂²

Because u = 0 and because both sides are equal to s₁ then g₁t₁² ₌ g₂t₂²

9.8 t₁² ₌ g₂ t₂²

9.8 t₁² ₌ g₂ (2t₁)²

g₂ = 2.45 ms^-2

 

Alternatively: on the surface, the time to fall 1.5 m from rest can be calculated from:

s₁ = ut₁ + ½ g₁t₁²

1.5 = 0 + ½ x ^-9.8 t₁²

t₁ = 0.553 s

As t₂ = 2 t₁ then t₂ = 1.107 s

s₁ = ut₂ + ½ g₂t₂²

1.5 = 0 + ½ x g₂ (1.107)²

g₂ = 2.45 s

 

g = Gm/d²

d² = Gm/g = 6.67 x 10^-11 x 6 x 10²⁴/2.45 = 1.6 x 10¹⁴

d = 1.28 x 10⁷ m

Distance above Earth = 1.28 x 10⁷ m - 6.38 x 10⁶ = 6400 km

 

The relationship to consider is: g µ m/d²

(a) half the mass but the same radius (or twice mass and twice radius etc).

(b) if t is twice normal then g would be ¼ normal, therefore: double the radius; keep mass constant.

(c) same as for answer (b)

 

g_(surface) = Gm/d² = Gm/(5.1 x 10⁶)² = Gm/(2.6 x 10¹³)

g_{(above surface)} = Gm/d² = Gm/(5.1 x 10⁶ + 150 x 10³)² = Gm/(2.76 x 10¹³)

g_{(above surface)}/g_(surface) = 2.6 x 10¹³/2.76 x 10¹³ = 0.94

 

r3	T2
7.5 x 1025	3.13
30.2 x 1025	12.60
122.5 x 1025	51.27
664.4 x 1025	278.89

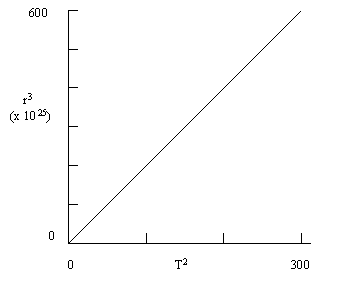
Graph is linear (passes through origin) hence r³ µ T²

 

(a)



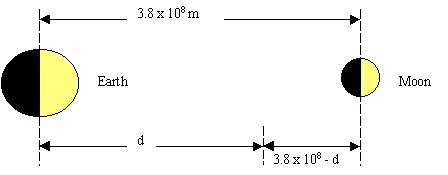
F_Moon = F_Earth

G m_em/d² = Gm_mm/(3.8 x 10⁸ - d)²

6 x 10²⁴/d² = 7.34 x 10²²/(3.8 x 10⁸ - d)²

Take square roots of both sides:

2.45 x 10¹²/d = 2.71 x 10¹¹/(3.8 x 10⁸ -d)

9.31 x 10²⁰ = 2.45 x 10¹² d = 2.71 x 10¹¹ d

9.31 x 10²⁰ = 2.72 x 10¹² d

d = 3.42 x 10⁸ m

 

(b) 0.89 of the distance to the Moon

(c) NO! In circular orbit you would experience free-fall and feel weightless.

 

(a) g = Gm/d² = 6.67 x 10^-11 x 6 x 10²⁴/(6.38 x 10⁶ + 10000)² = 9.8011 ms^-2

No noticable difference.

(b) Same as on the Earth's surface - no difference.

 

(a) g = Gm/d² = 6.67 x 10^-11 x 2.0 x 10³⁰/(12 x 10³)² = 9.2 x 10¹¹ ms^-2

(b) v = 2p r/T = 2 p x 12 x 10³/0.041 = 1.84 x 10⁶ ms^-1

a_c = v²/r = (1.84 x 10⁶)²/ 1.2 x 10³ = 2.8 x 10⁸ ms^-2

 

Spring clock would not be affected by gravity and therefore will keep time. A pendulum is affected by gravity and won't keep time. The greater the gravitational force the faster the pendulum will oscillate.

 

r_e = 6.38 x 10⁶ m

r_b (radius for Brisbane) = r_e cos 28° = 6.38 x 10⁶ x cos 28° = 5.63 x 10⁶ m

(a) circumference = 2 p r = 2 p x 5.63 x 10⁶ = 3.54 x 10⁷ m

(b) v = s/t = 3.54 x 10⁷/ (24 x 3600) = 410 ms^-1

(c) a_c = v²/r = 410²/5.63 x 10⁶ = 0.030 ms^-2

(d) F_C = ma_c = 60 x 0.030 = 1.79 N

(e) (i) Gravitational force F_G points towards the centre of the Earth (see figure that follows):



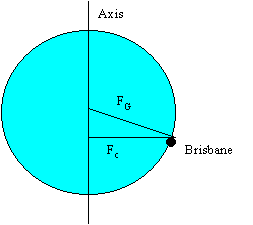
(ii) Perp. to Earth's axis through Brisbane (see figure that follows):



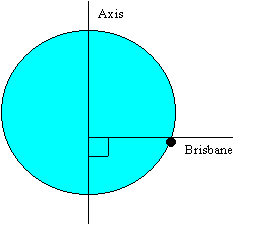
(iii) Perp. to Earth's axis through Brisbane (see figure for (ii) above).
 

Question 58

v = √(2Gm/r) = √(2 x 6.67 x 10^-11 x 1.4 x 10¹¹ x 2 x 10³⁰)/(80000 x 3600 x 24 x 365 x 3 x 10⁸)
   = (3.73 x 10³¹)/(7.57 x 10²⁰) = 4.93 x 10¹⁰ m/s (greater than "c" so can't escape).

Question 59

r = 9.4 x 10⁶m
T = 7h 39m = 7.65h = 2.754 x 10⁴ s
v = √(2pr/T) = (5.9 x 10⁷/(2.754 x 10⁴) = 2.14 x 10³ m/s

F_c= mv²/r = Gm₁m₂/r²
v² = Gm/r
m = v²r/G = (2.14 x 10³)² x 9.4 x 10⁶/(6.67 x 10^-11)
m = 6.475 x 10²³ kg

Question 60

(a) l_p = 0.0029/T = 0.0029/7600 = 3.8 x 10^-7 m
     l_f = 0.0029/T = 0.0029/7600 = 3.8 x 10^-7 m
(b) Procycon as it has bigger surface area.
(c) Same temp, same area, hence same rate of emission.