Chapter 9 - Worked Solutions

to questions from the OUP text Senior Physics - Concepts in Context by Walding, Rapkins and Rossiter

My thanks to Peter Finch from St Joseph's College, Gregory Terrace, for these (pdf) solutions.

Solutions-Ch9-Finch.pdf

The rest are by me, Richard Walding:

Question 34

(a) p_i = p_f
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
1.6 x 5.5 + 2.4 x 2.5 = 1.6 v₁ + 2.4 x 4.9
14.8 = 1.6 v₁ + 11.76
v₁ = 1.9 ms^-1 (assuming the positive direction is to the right).

(b) Initial kinetic energy E_K(i) = ½ m₁u₁² + ½ m₂u₂² = ½ x1.6 x 5.5² + ½ 2.4 x 2.5² = 31.7 J
Final kinetic energy E_K(f) = ½ m₁v₁² + ½ m₂v₂² = ½ x 1.6 x 1.9² + ½ x 2.4 x 4.9² = 31.7 J
As E_K(i) = E_K(f) the collision is elastic.
 
(c) No. Mathematically v₁ would equal - 3.9 ms^-1 and v₂ would equal + 3.8 ms^-1.
 
PROOF: u₁ = +5.5 ms^-1; u₂ = -6 ms^-1

Conservation of momentum:

p_i = p_f
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
2.8 = 1.6 v₁ + 2.4 v₂
v₁ = 1.75 - 1.5 v₂
 

Conservation of kinetic energy:

E_K(i) = E_K(f)
½ m₁u₁² + ½ m₂u₂² = ½ m₁v₁² + ½ m₂v₂²
39.6 = v₁² + 1.5v₂²
39.6 = (1.75 - 1.5 v₂)² + 1.5 v₂²
v₂² - 1.39 v₂ = 9.74 = 0
 

Using the quadratic formula there are two solutions: v₁ = +2.5 ms^-1 and hence v₂ = -0.5 ms^-1.
This is impossible as the balls would have to had jumped over each other.
 
The second solution: v₁ = -3.9 ms^-1 and hence v₂ = +3.8 ms^-1. In this case Ball 1 is travelling in the negative direction and hence can't be travelling in the positive direction.
 

Part (a) Prove vertical displacement is 7.3 cm:

Solving for side of triangle (200 - h) = 192.7 cm, hence h = 7.3 cm


Part (b) Calculate velocity:

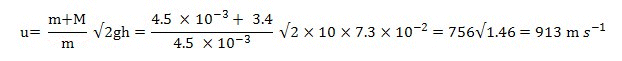
Which is quite fast. (A big thank you to Chris Smith at Sunshine Coast Grammar School for pointing out my poor proofreading).

Question 36

GPE = mgh = 5.5 x 10⁶ x 10 x 50 = 2.75 x 10⁹ J (= 2750 MJ)
At 2 cents per MJ this comes to $55 per second or $4.75 million per day.
 

Question 37

(a) 1 MJ = 1/31 litres = 0.0322 L
Distance = 100/11.5 x 0.0322 = 0.28 km
 
(b) 60 km/h = 60/100 x 11.5 litres/hour = 6.9 L/hr
Power = 6.9 x 31 MJ per hour = 214 MJ/hr = 2.14 x 10⁸ J/hr
Joules per second = J/hr divided by 3600
= 2.14 x 10⁸/3600 =5.94 x 10⁴ J/s = 5.94 x 10⁴ Watts).
 

Question 38

E_K(i) = ½ mv² = ½ x 0.63 x 14² = 61.74 J
GPE = mgh = 0.63 x 10 x 8.1 = 51.03 J
Work done = 61.74 - 51.03 = 10.7 J
 

Question 39

assume all GPE converted to EPE
mgh = ½ kx²
1587 x 10 x 180 = ½ k (180 - 30)²
k = 254 Nm
 

Question 40

 
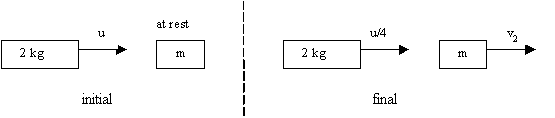
Conservation of Momentum: p_i = pf

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
2 u = 2u/4 + mv₂
3/2 u = mv₂
u = 2 mv₂/3
 

Conservation of Kinetic Energy: E_K(i) = EK(f)

½ m₁u₁² + ½ m₂u₂² = ½ m₁v₁² + ½ m₂v₂²
½ x u² + 0 = ½ x 2 x (u/4)² + ½ mv₂²
2u² = 2u²/16 + mv₂²
2u² - 2/16 u² = mv₂²
30/16 u² = mv₂²
u² = 16mv₂²/30
 

From momentum: u = 2 mv₂/3, therefore u² = 4 m²v₂²/9
Hence 4 m²v₂²/9 = 16mv₂²/30
Cancel v₂² from both sides:
4 m²/9 = 16 m/30
120 m = 144
m = 1.2 kg
 

Question 41

D KE = D GPE
D GPE = mgh = 1586 x 10³ x 10 x 1.2 = 1.9 x 10⁷ J
D KE = ½ m (v² - u²) = - 1.9 x 10⁷ J
½ x 1586 x 10³ (v² - (28000/3600)²) = - 1.9 x 10⁷ J
793000 (v² - 60.5) = - 1.9 x 10⁷ J
793000 v² - 4.8 x 10⁷ = - 1.9 x 10⁷ J
v = 6.0 ms^-1 (21.7 km h^-1

Question 42

EPE = ½ kx² = ½ mv²
½ x 292 x (3.2 x 10^-2)² = ½ x 12 x 10^-3 x v²
v = 5 ms^-1

Return to Physics Text Home Page